高中||數學必考的10條公式,想拿高分就得牢背!
數學公式就是解難題的鑰匙,也是想解題思路的基礎,高中數學學習和考試里,那些老用的公式,更是決定分數高低的關鍵,不管是畫函數圖像、算幾何圖形,還是分析概率統計,都得靠公式用得準,想在數學考試里突破瓶頸、拿高分,必考公式一定要記牢。下面就說說高中數學必須掌握的 10 條公式,幫你打好高分基礎。

一、數學必考的 10 條公式
1 .適用條件
[直線過焦點],必有ecosA=(x-1)/(x+1),其中A為直線與焦點所在軸夾角,是銳角。x為分離比,必須大于1。
注:上述公式適合一切圓錐曲線。如果焦點內分(指的是焦點在所截線段上),用該公式;如果外分(焦點在所截線段延長線上),右邊為(x+1)/(x-1),其他不變。
2 . 函數的周期性問題(記憶三個)
(1)若f(x)=-f(x+k),則T=2k;
(2)若f(x)=m/(x+k)(m不為0),則T=2k;
(3)若f(x)=f(x+k)+f(x-k),則T=6k。
注意點:a.周期函數,周期必無限b.周期函數未必存在最小周期,如:常數函數。c.周期函數加周期函數未必是周期函數,如:y=sinxy=sin派x相加不是周期函數。
3 . 關于對稱問題(無數人搞不懂的問題)總結如下
(1)若在R上(下同)滿足:f(a+x)=f(b-x)恒成立,對稱軸為x=(a+b)/2
(2)函數y=f(a+x)與y=f(b-x)的圖像關于x=(b-a)/2對稱;
(3)若f(a+x)+f(a-x)=2b,則f(x)圖像關于(a,b)中心對稱
4 . 函數奇偶性
(1)對于屬于R上的奇函數有f(0)=0;
(2)對于含參函數,奇函數沒有偶次方項,偶函數沒有奇次方項
(3)奇偶性作用不大,一般用于選擇填空
5 . 數列爆強定律
(1)等差數列中:S奇=na中,例如S13=13a7(13和7為下角標);
(2)等差數列中:S(n)、S(2n)-S(n)、S(3n)-S(2n)成等差
(3)等比數列中,上述2中各項在公比不為負一時成等比,在q=-1時,未必成立
(4)等比數列爆強公式:S(n+m)=S(m)+q2mS(n)可以迅速求q
6 . 數列的終極利器,特征根方程
首先介紹公式:對于an+1=pan+q(n+1為下角標,n為下角標),
a1已知,那么特征根x=q/(1-p),則數列通項公式為an=(a1-x)p2(n-1)+x,這是一階特征根方程的運用。
二階有點麻煩,且不常用。所以不贅述。希望同學們牢記上述公式。當然這種類型的數列可以構造(兩邊同時加數)
7 . 函數詳解補充
1、復合函數奇偶性:內偶則偶,內奇同外
2、復合函數單調性:同增異減
3、重點知識關于三次函數:恐怕沒有多少人知道三次函數曲線其實是中心對稱圖形。
它有一個對稱中心,求法為二階導后導數為0,根x即為中心橫坐標,縱坐標可以用x帶入原函數界定。另外,必有唯一一條過該中心的直線與兩旁相切。
8 . 常用數列bn=n×(22n)求和Sn=(n-1)×(22(n+1))+2記憶方法
前面減去一個1,后面加一個,再整體加一個2
9 . 適用于標準方程(焦點在x軸)爆強公式
k橢=-{(b2)xo}/{(a2)yo}k雙={(b2)xo}/{(a2)yo}k拋=p/yo
注:(xo,yo)均為直線過圓錐曲線所截段的中點。
10 . 強烈推薦一個兩直線垂直或平行的必殺技
已知直線L1:a1x+b1y+c1=0直線L2:a2x+b2y+c2=0
若它們垂直:(充要條件)a1a2+b1b2=0;
若它們平行:(充要條件)a1b2=a2b1且a1c2≠a2c1[
這個條件為了防止兩直線重合)
注:以上兩公式避免了斜率是否存在的麻煩,直接必殺!
二、西安伊頓教育數學一對一好嗎?
西安伊頓教育數學一對一教學質量挺高的,數學老師大多是重點院校畢業,專業知識扎實,還有多年教學經驗,對高考命題趨勢和考試大綱研究得很透。他們注重根據學生情況來教,老師課前會和學生好好溝通,了解學習情況、習慣和目標,然后制定個性化教學計劃,上課的時候,老師會密切關注學生反應,隨時調整教學節奏和方法。基礎差的學生,老師會從最簡單的題型開始教,慢慢幫孩子把知識漏洞補上;成績好的學生,就重點講提分技巧和難題解法。
西安伊頓教育咨詢熱線:
- 熱門課程
- 熱門資訊
- 熱門資料
- 熱門福利
-
 常用英語詞組(短語)及固定搭配大全英語學習,詞匯是基礎,短語和固定搭配才是靈魂。很多家長和學生在積累單詞的同時,卻忽略了短語的運用,導致“會認不會用”。為此,我們特別整理了一份覆蓋廣泛的高頻英語短語+固定搭配大全,附帶實用例句,幫助孩子真正做到“詞組開口就來”! 一、必備短語 1. an amount of +不可數名詞
常用英語詞組(短語)及固定搭配大全英語學習,詞匯是基礎,短語和固定搭配才是靈魂。很多家長和學生在積累單詞的同時,卻忽略了短語的運用,導致“會認不會用”。為此,我們特別整理了一份覆蓋廣泛的高頻英語短語+固定搭配大全,附帶實用例句,幫助孩子真正做到“詞組開口就來”! 一、必備短語 1. an amount of +不可數名詞 -
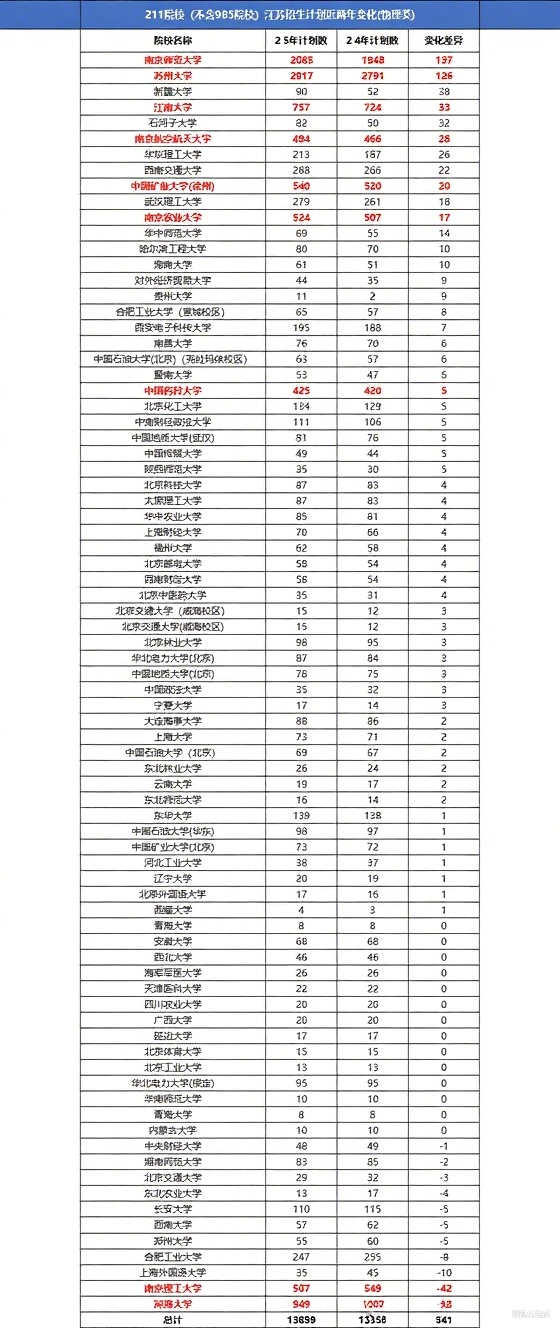 2025年江蘇高考211院校錄取全景:分數位次+計劃增減今天,咱們來聊聊除了 985 大學之外的 211 院校在江蘇的招生情況,看看江蘇考生要考多少分才能進 211 大學。 一、211 院校錄取名額表 今年,211 高校在江蘇物理類普通本科批一共招 14423 人,比去年的 13865 人多了 558 個名額。 二、哪類孩子適合報秦學伊頓教
2025年江蘇高考211院校錄取全景:分數位次+計劃增減今天,咱們來聊聊除了 985 大學之外的 211 院校在江蘇的招生情況,看看江蘇考生要考多少分才能進 211 大學。 一、211 院校錄取名額表 今年,211 高校在江蘇物理類普通本科批一共招 14423 人,比去年的 13865 人多了 558 個名額。 二、哪類孩子適合報秦學伊頓教 -
 張雪峰深夜爆料!文科生只有這3個專業不失業,選錯毀一生2024 年文科生找工作太難了,人文學科畢業生簽約率才 12.4%,這數兒讓好多家長睡不著覺,張雪峰在最近直播里說得很直接,文科生想不失業,就三條路能走,選錯了,真的會后悔一輩子。 一、文科生推薦學的三個專業 漢語言文學:漢語言文學就是學文學欣賞、怎么寫東西、語言規律這些主要內容,能系統提高
張雪峰深夜爆料!文科生只有這3個專業不失業,選錯毀一生2024 年文科生找工作太難了,人文學科畢業生簽約率才 12.4%,這數兒讓好多家長睡不著覺,張雪峰在最近直播里說得很直接,文科生想不失業,就三條路能走,選錯了,真的會后悔一輩子。 一、文科生推薦學的三個專業 漢語言文學:漢語言文學就是學文學欣賞、怎么寫東西、語言規律這些主要內容,能系統提高 -
 體育單招文化課逆襲?伊頓單招有方法!體育生天天訓練,場上倒是挺厲害,可文化課老是拖后腿,好多人因為成績不夠,跟想上的大學擦肩而過。不過別擔心,伊頓單招早就專門針對體育生文化課的問題,弄出了一套管用的辦法,讓以前的弱項變成加分項,幫你穩穩過單招這關。
體育單招文化課逆襲?伊頓單招有方法!體育生天天訓練,場上倒是挺厲害,可文化課老是拖后腿,好多人因為成績不夠,跟想上的大學擦肩而過。不過別擔心,伊頓單招早就專門針對體育生文化課的問題,弄出了一套管用的辦法,讓以前的弱項變成加分項,幫你穩穩過單招這關。
-
 高考作文素材積累:流浪詩人——我的人生之路各位學生注意了,現在就要進入到2023年陰歷新年,各位學生過完年距離中高考又進了一步,為方便大家能夠積累更多的作文素材,小編老師為定期為大家更新優秀范文,下面大家一起來賞析“流浪詩人——我的人生之路”。 作文題 閱讀下面的材料,根據要求寫一篇不少于800字的文章。(60分) 黃大發,一位普
高考作文素材積累:流浪詩人——我的人生之路各位學生注意了,現在就要進入到2023年陰歷新年,各位學生過完年距離中高考又進了一步,為方便大家能夠積累更多的作文素材,小編老師為定期為大家更新優秀范文,下面大家一起來賞析“流浪詩人——我的人生之路”。 作文題 閱讀下面的材料,根據要求寫一篇不少于800字的文章。(60分) 黃大發,一位普 -
 2023年高考作文素材積累:“絕品即常品”各位學生大家覺得高考作文多少分才過關呢?小編老師覺得作文滿分60分大家作文在56分以上才算是過關,大家都知道高考一分之差差之千里,大家不要放過任何一個可以提分的可能!為幫助大家積累素材,小編老師為大家整理了比較好的作文題目和作文范文,供大家參考! 作文題 閱讀下面的材料,根據要求寫一篇不
2023年高考作文素材積累:“絕品即常品”各位學生大家覺得高考作文多少分才過關呢?小編老師覺得作文滿分60分大家作文在56分以上才算是過關,大家都知道高考一分之差差之千里,大家不要放過任何一個可以提分的可能!為幫助大家積累素材,小編老師為大家整理了比較好的作文題目和作文范文,供大家參考! 作文題 閱讀下面的材料,根據要求寫一篇不 -
 高考英語素材,高考英語作文開頭常用句子高考英語素材,高考英語作文開頭常用句子!一提到英文寫作,很多同學就頭疼,如何組織語言、如何下筆呢?但自從知道了一些萬能的“套話”你就會發現自己的寫作水平會更上一層樓!下面小編老師為大家整理了高考英語作文開頭常用句子,想要了解的學生收藏起來! 開頭常用句子 1.Depending on per
高考英語素材,高考英語作文開頭常用句子高考英語素材,高考英語作文開頭常用句子!一提到英文寫作,很多同學就頭疼,如何組織語言、如何下筆呢?但自從知道了一些萬能的“套話”你就會發現自己的寫作水平會更上一層樓!下面小編老師為大家整理了高考英語作文開頭常用句子,想要了解的學生收藏起來! 開頭常用句子 1.Depending on per -
 西安高三化學輔導班哪家好?化學現在在新高考的分量也比較重,很多專業都要求選擇化學這門課。與物理相比化學不算難。最近有學生問老師西安高三化學輔導班哪家好?下面,小編老師為大家推薦西安一家比較好的高中補習機構,大家了解一下: 伊頓教育高三·化學輔導 基礎 1.激發學習動機2.培養學習興趣3.化學方程式總結歸納
西安高三化學輔導班哪家好?化學現在在新高考的分量也比較重,很多專業都要求選擇化學這門課。與物理相比化學不算難。最近有學生問老師西安高三化學輔導班哪家好?下面,小編老師為大家推薦西安一家比較好的高中補習機構,大家了解一下: 伊頓教育高三·化學輔導 基礎 1.激發學習動機2.培養學習興趣3.化學方程式總結歸納




















 All right reserved
All right reserved
